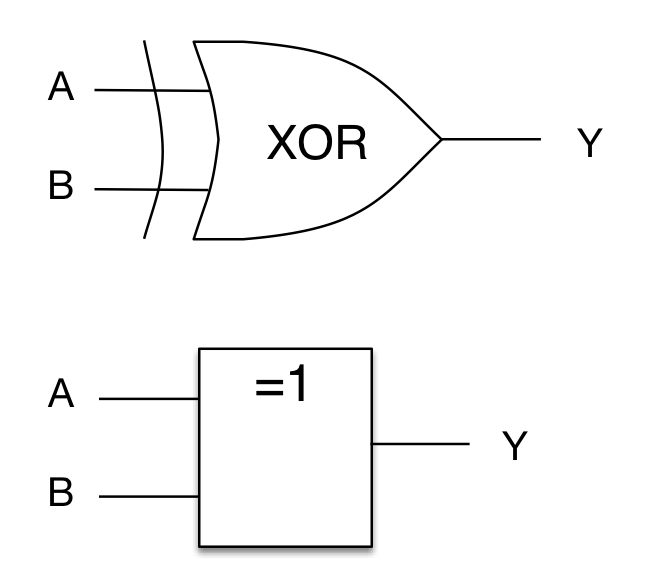
In digital electronics and software, we often meet the XOR function, also known as the Exclusive OR. This differs from the inclusive OR. The logic symbols for an electronic XOR gate are as follows:
The truth table for XOR is as follows:
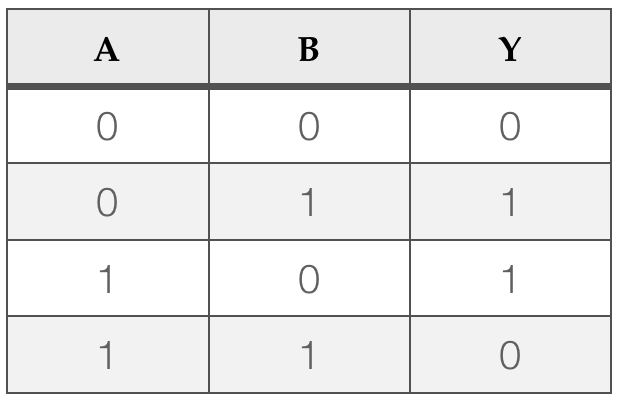
In words, the output is 1 if one and only one input is set to 1. Some observations about this:
- If you XOR a bit ‘A’ with a 1, then the result is always a the opposite state (toggle)
- If you XOR a bit ‘A’ with a 0, then the result is A (preserved)
We use these properties to toggle or preserve individual or groups of bits
This is not limited to single bits. In software, we often perform logical operations on integers (binary numbers). Consider the following example:
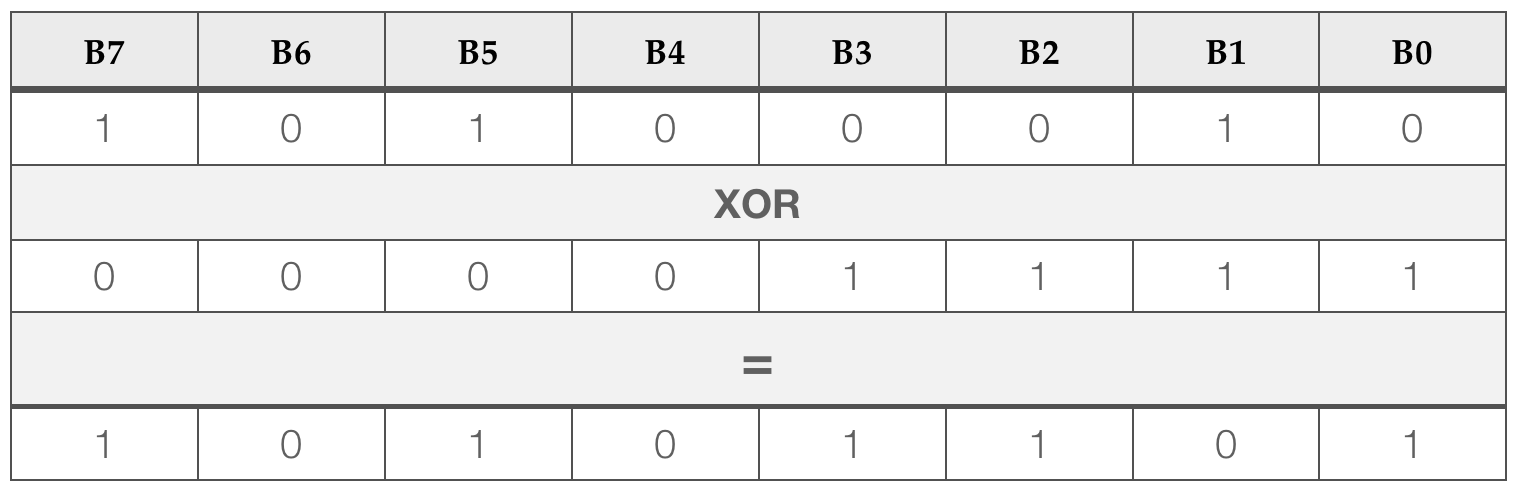
The XOR function is applied to each pair of bits. In the C or C++ programming language, this could be calculated as:
unsigned A = 162; //A2 IN HEX A = A ^ 15;
The result is 173 //AD IN HEX